通过快排模拟IDE上qosrt的实现方法
-
前言
排序是编程中经常用到的数据处理方法,比如说我们可能要对实验数据进行分析,对高考成绩进行排名,在嵌入式领域中,常常要对MCU中ADC采集的数据进行排序处理,具有高频出现的特征,所以好的排序方法对于数据处理的准确,提升程序运行效率具有重要的意义。一般我们常用的排序方法有一下几种,插入排序,选择排序,冒泡排序,快速排序等等,其中Visual Studio提供了快速排序的API,我们可以方便调用qsort,但是我们点进去函数定义时可以发现,VS只提供了接口,而没有展示具体实现,下面,我尝试通过我对排序算法的一些理解,模拟一下qsort的实现。

qsort原理介绍
排序目前主要有以下几种算法,插入排序,选择排序,冒泡排序,快速排序算法,其中插入排序,选择排序,冒泡排序算法的时间复杂度为O(n^2),在处理大量数据时效率不高,而快速排序的时间复杂度比较低,为O(log2N),所以我选择通过快速排序算法,模拟Visual Studio IDE中的实现。快速排序采用的是分而治之的思想,每次从数组中取一个元素作为基准值,将小于基准值的元素放左边,大于基准值的元素放右边,通过对左,右区域进行迭代操作,最终实现排序。示意图如下:
 ![51b3f240-6478-44f3-9065-0e0f08c2c334-image.png]
![51b3f240-6478-44f3-9065-0e0f08c2c334-image.png]
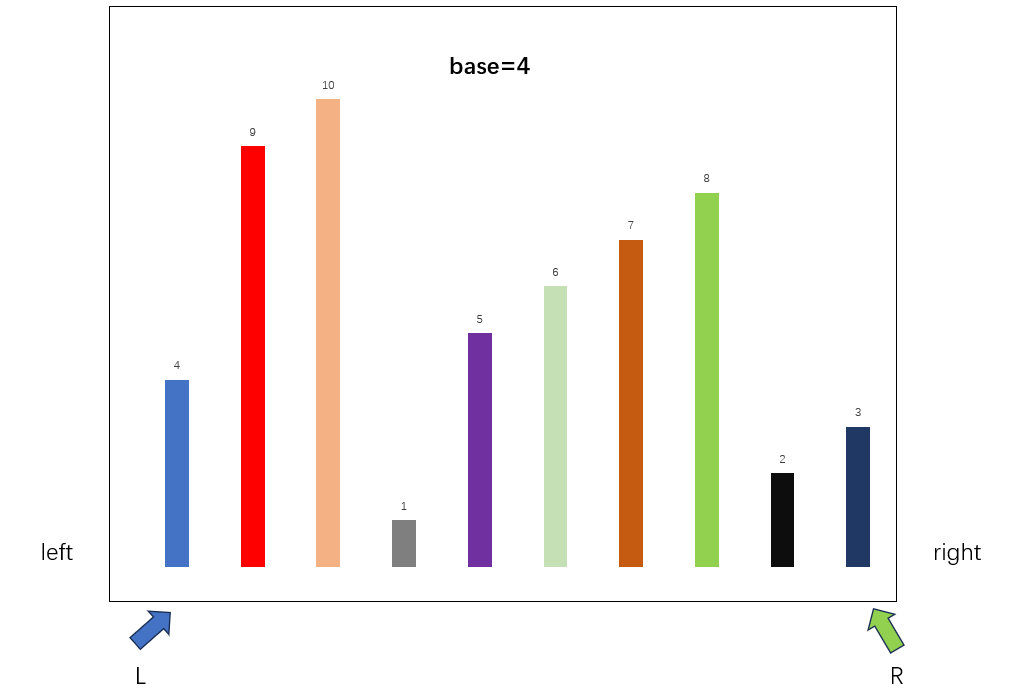
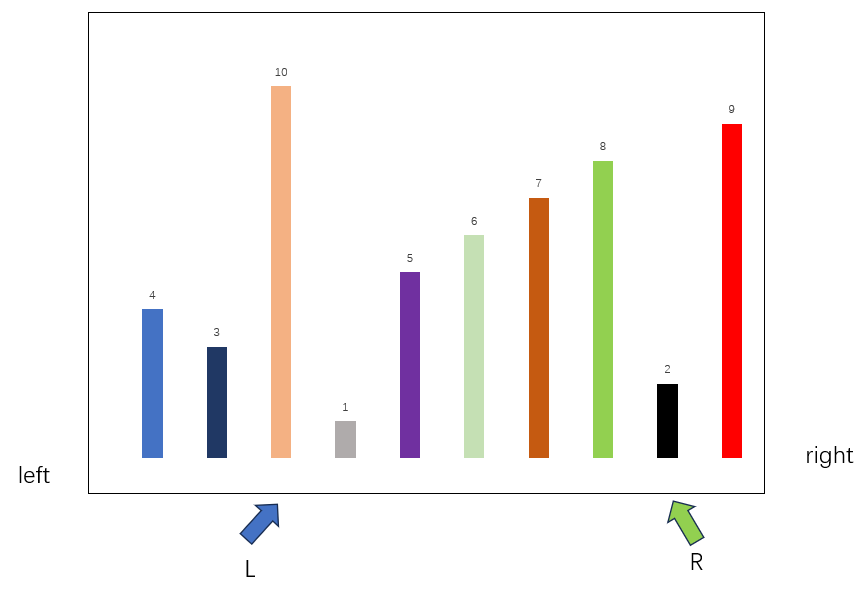
先确定本次排序的数组边界,分别是left,right,随后初始化指针L,R,分别指向本轮迭代的边界,将比较基准设置为数组第一个元素,在本轮迭代中,base=4,随后开始查找数组元素交换,将R向左移动,寻找比base小的数据,将L向右移动,寻找比base大的数据,当两者都找到合适的数据后,互相交换,即可实现排序。
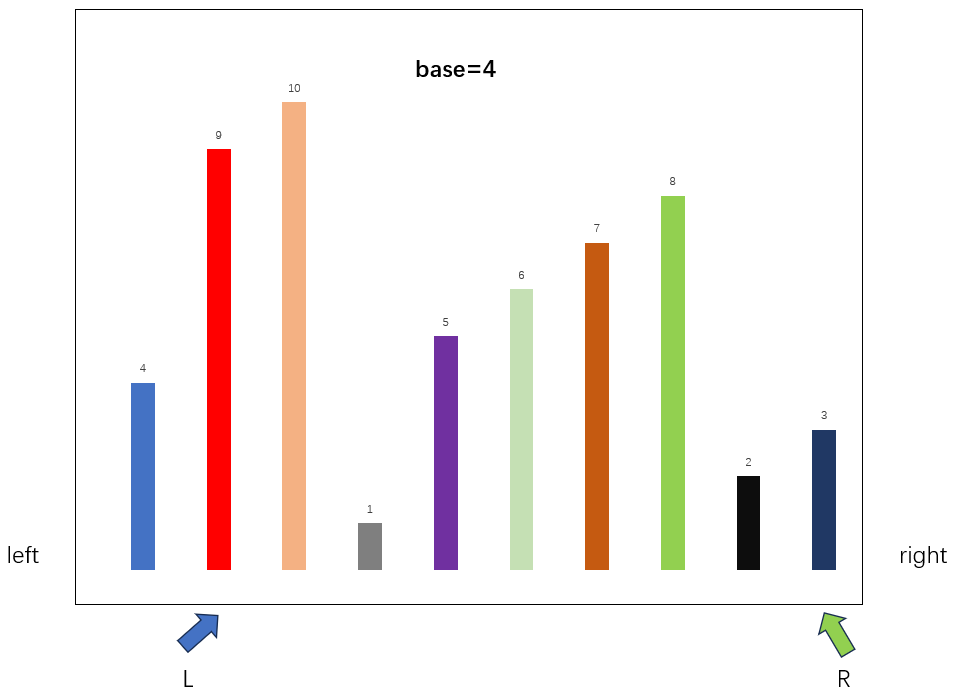
交换
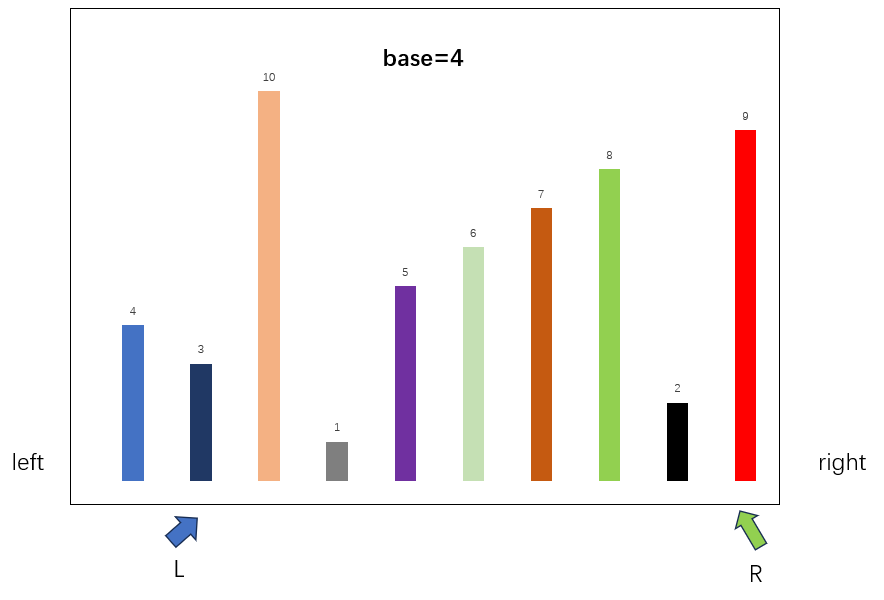
继续查找下一组合适的元素
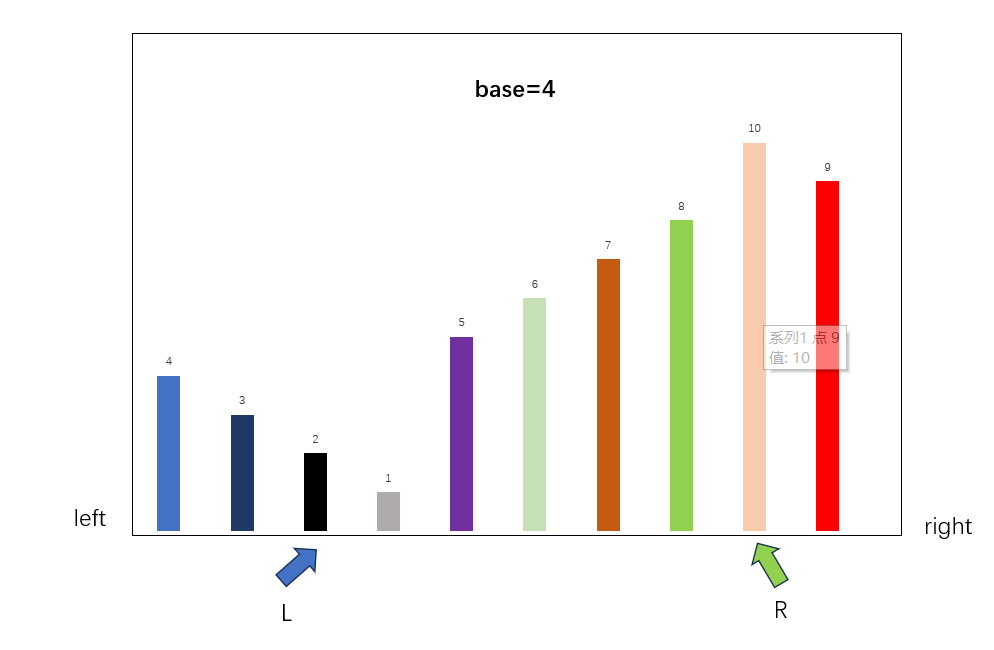
交换
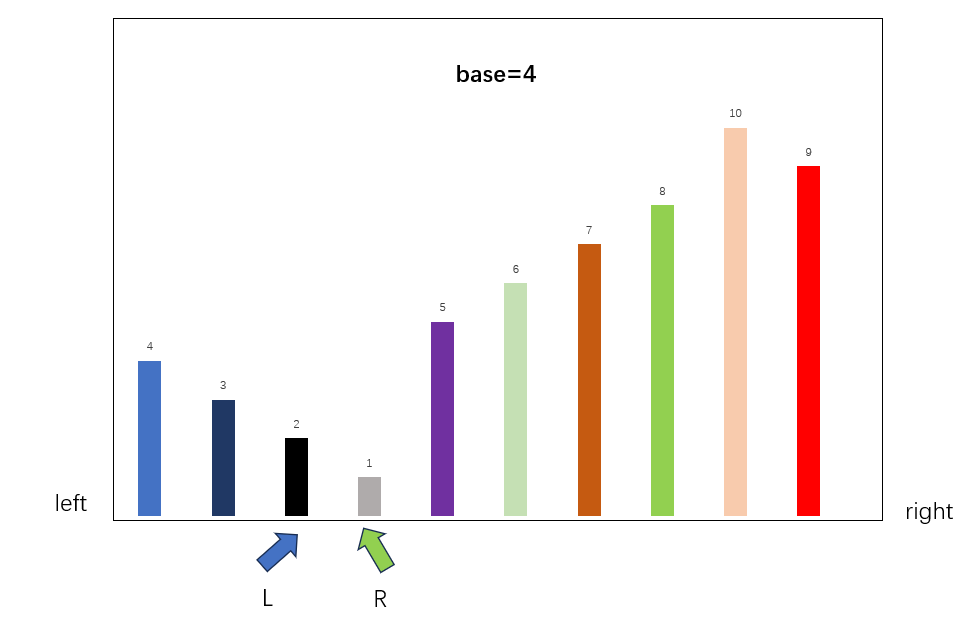
依此类推(注意是要先移动右边的R指针,确定其符合要求再移动左边的指针)
此时右移动L指针,L和R重叠,无法满足交换条件,证明R指针右边的数都比Base大,于是交换Base和R,进行下一轮排序
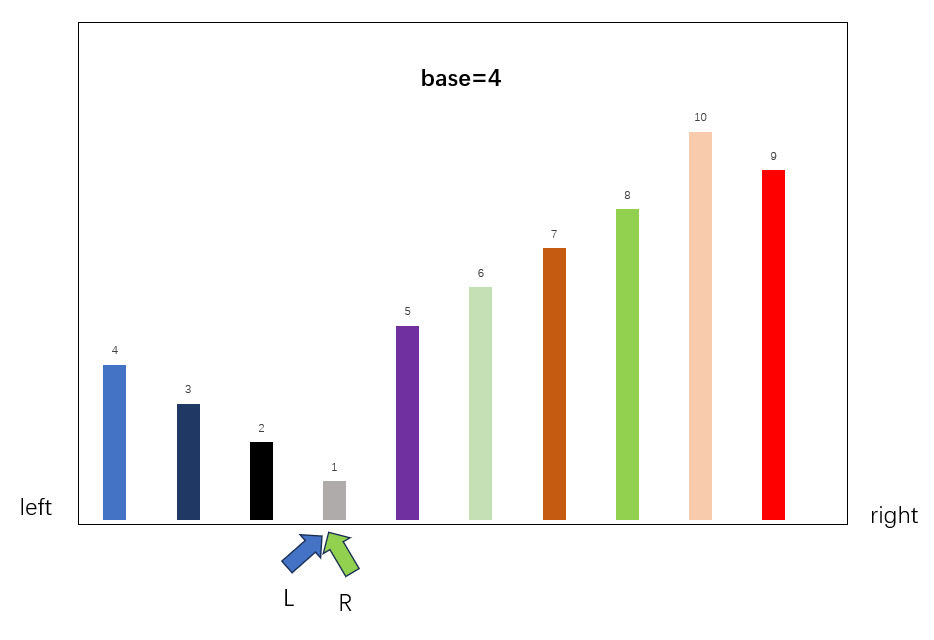
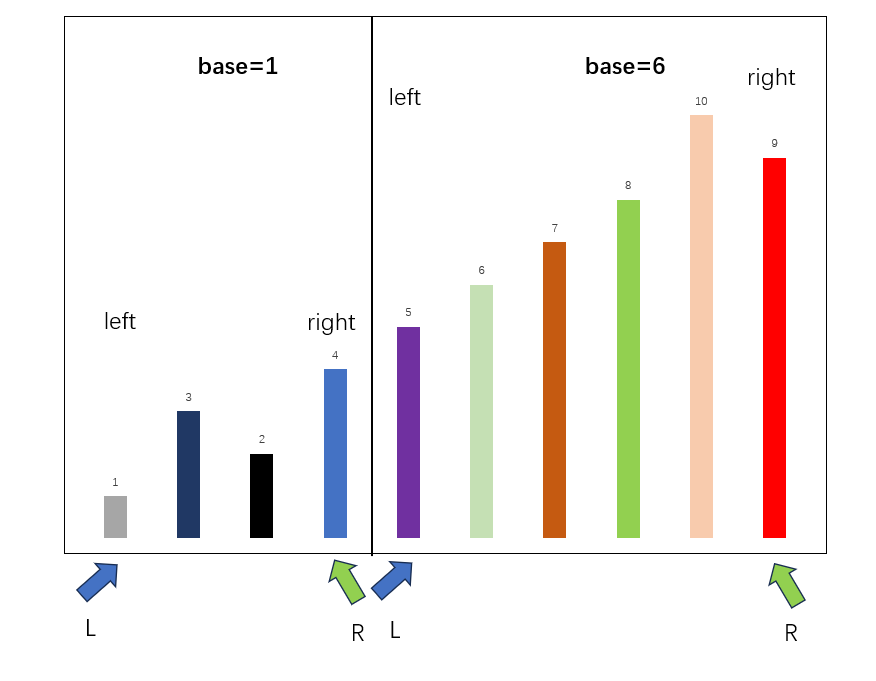
通过不断迭代,我们每次将排序范围缩少一般,所以经过O(log2N)次,我们即可实现排序。
代码具体实现如下void my_qsort(uint8_t array[], uint8_t left, uint8_t right) { int base = array[left]; uint8_t L = left; uint8_t R = right; while (L < R) { while ((array[R] > base)&&L<R) { R--; } while ((array[L] <= base)&&L<R) { L++; } uint8_t temp; temp = array[R]; array[R] = array[L]; array[L] = temp; } uint8_t temp; temp = array[L]; array[L] = array[left]; array[left] = temp; if(left<L) my_qsort( array, left, L-1); if(R<right) my_qsort( array, R+1, right); }int main() { uint8_t array[10] = { 0 }; srand((unsigned)time(NULL)); for (int i = 0; i < 10; i++) { array[i] = i+1; } for (int i = 0; i < 5; i++) //生成无序随机数 { uint8_t j = rand() % 10; uint8_t k = rand() % 10; uint8_t temp; temp = array[k]; array[k] = array[j]; array[j] = temp; } printf("data:"); for (int i = 0; i < 10; i++) { printf("%d ", array[i]); } printf("\r\n"); my_qsort(array,0,9); //进行排序 printf("after sort:"); for (int i = 0; i < 10; i++) { printf("%d ", array[i]); } }看看运行效果

但是,这个函数形式跟Visual Studio提供了快速排序的API还有较大区别,探索完原理后我们还需要将快排算法,写成Visual Studio提供API的形式。qsort的具体实现
_ACRTIMP void __cdecl qsort(
Inout_updates_bytes(_NumOfElements * _SizeOfElements) void* _Base,
In size_t _NumOfElements,
In size_t _SizeOfElements,
In _CoreCrtNonSecureSearchSortCompareFunction _CompareFunction
);首先,我们观察qsort的传参部分,其参数有未定义类型指针Base(指向需要比较元素的地址),_NumOfElements(需要比较的元素数量),_SizeOfElements(元素的字节大小),_CompareFunction(函数指针,确定元素的比较方法)
将我们自己编写的my_qsort和qsort对比即可知道,我们如何改写自己的函数。
观察void my_qsort(uint8_t array[], uint8_t left, uint8_t right),参数指针array(指向需要比较的元素地址),left(需要比较的起始元素下标),right(需要比较元素的终止下标),其实到这里,就比较清晰了,参数array跟base其实是一样的,指代比较元素的内存地址所在,_NumOfElements=right-left,指代需要比较元素的数量,_SizeOfElements指元素字节的大小,由于我们自己写的my_qsort是指定单字节的数字比较,可是在实践中,我们常常会有uint16_t,uint32_t甚至是float的比较需求,所以我们可以看到IDE提供的API还是有很大的灵活性,可以对比各种元素,_CompareFunction指元素的对比规则,是升序还是降序,我们下面可以结合具体代码进行分析。
my_qsort是这样定义基准的:
int base = array[left];
uint8_t L = left;
uint8_t R = right;将其转换为qsort可以这样写,
uint8_t L = 0;
uint8_t R = numofElement-1;
这样可以同样得到,L和R指针的下标,随后进行比较while (L < R) { while ((array[R] > base)&&L<R) { R--; } while ((array[L] <= base)&&L<R) { L++; } uint8_t temp; temp = array[R]; array[R] = array[L]; array[L] = temp; }可以这样改写
while (L < R) { while (CompareFunction((unsigned char*)base + (R * sizeofElement), (unsigned char*)base)>0 && L < R) //array[R] > base { R--; } while (CompareFunction((unsigned char*)base + (L * sizeofElement), (unsigned char*)base) <= 0 && L < R) //array[L] <= base { L++; } for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement)+i; unsigned char* buf2 = (unsigned char*)base + (R * sizeofElement)+i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; } }从这里可以看到,sizeofElement的作用就发挥出来了,我们自己实现的my_qsort是array[R] > base进行比较,但是我们这里比较只知道起始地址base和字节大小sizeofElement,但是我们知道数据地址和数据类型,我们就可以求得其元素,我们平时的指针操作就是这样的。
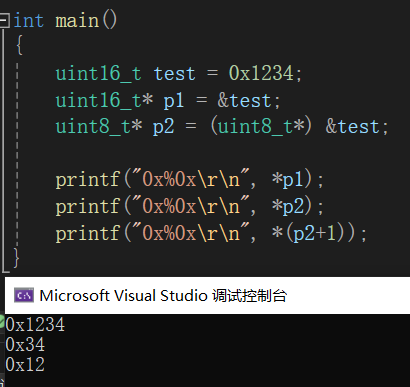
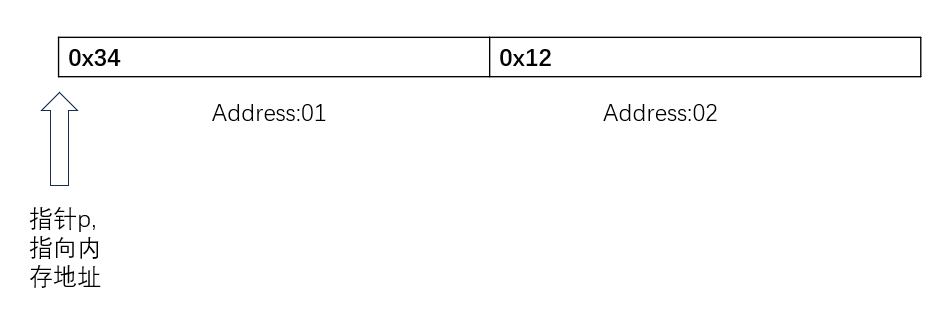
当指针p1指向address:01时,并按照uint16_t进行解释,就是把两个字节的内存数据进行整合分析,所以打印结果是0x1234,当指针p2指address:01时,并按照uint8_t进行解释时,解释的是单字节,所以打印结果是0x34,当p2在内存移动,p2+1时,p2指向address:02地址时,解释为0x12,当然,数据在内存上的分布,跟硬件的大小端有关,这里不展开解释,所以通过(地址+数据类型)的方法,我们可以得到数据大小,并进行比较,而不用像我们的my_qsort函数一样只能固定比较无符号8位数。
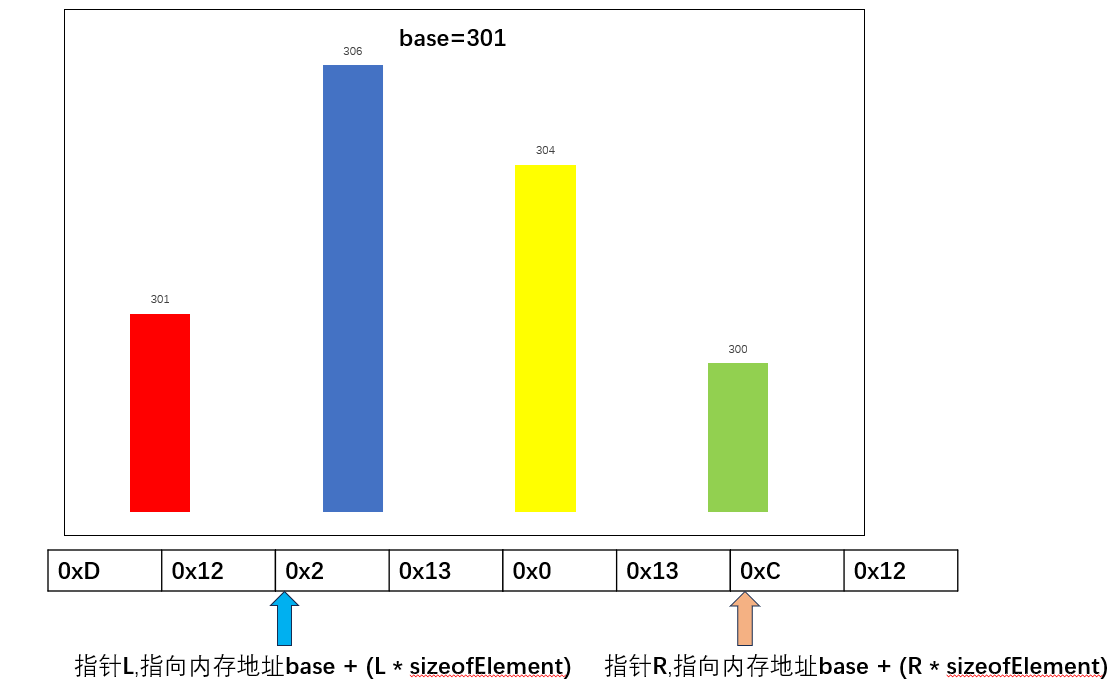
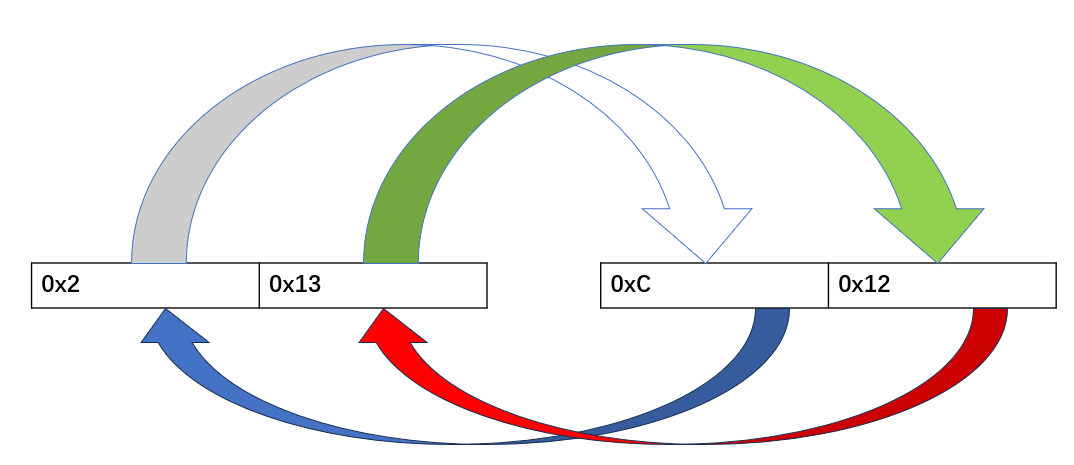
起始地址为base,由于我们的数据是300已经超过了uint8_t的范围,所以只能采用uint16_t,所以,一个数据占用2个字节,即是sizeofElement为2,base=301,R指针指向最后一个数300,其地址为base + (3 * sizeofElement),下标为3,L指针指向306,其地址为base + (1* sizeofElement),跟我们用数组其实是一个寻址原理,然后进行交换for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement)+i; unsigned char* buf2 = (unsigned char*)base + (R * sizeofElement)+i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; }我们交换通过逐字节交换,数量为sizeofElement,最终实现数组元素交换
随后,进行迭代递归,即可完成,下面的函数完整代码void test_qsort(void* base,uint8_t numofElement,uint8_t sizeofElement, strcmp_fun CompareFunction) { uint8_t L = 0; uint8_t R = numofElement-1; while (L < R) { while (CompareFunction((unsigned char*)base + (R * sizeofElement), (unsigned char*)base)>0 && L < R) //array[R] > base { R--; } while (CompareFunction((unsigned char*)base + (L * sizeofElement), (unsigned char*)base) <= 0 && L < R) //array[L] <= base { L++; } for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement)+i; unsigned char* buf2 = (unsigned char*)base + (R * sizeofElement)+i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; } } for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement) + i; unsigned char* buf2 = (unsigned char*)base+i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; } if (base < (unsigned char*)base + (L * sizeofElement)) test_qsort(base,L , sizeofElement, CompareFunction); if ((unsigned char*)base + (R * sizeofElement) < (unsigned char*)base + (numofElement-1) * sizeofElement) test_qsort((unsigned char*)base+(R+1)* sizeofElement, numofElement-L-1,sizeofElement, CompareFunction); }我们在IDE上运行测试一下代码:
typedef int (*strcmp_fun)(const void*,const void*); int CompareFunction(const void*, const void*); void test_qsort(void* base, uint8_t numofElement, uint8_t sizeofElement, strcmp_fun CompareFunction); int main() { uint16_t array[10] = { 0 }; srand((unsigned)time(NULL)); for (int i = 0; i < 10; i++) { array[i] =rand()%1000; } for (int i = 0; i < 5; i++) //生成无序随机数 { uint8_t j = rand() % 10; uint8_t k = rand() % 10; uint8_t temp; temp = array[k]; array[k] = array[j]; array[j] = temp; } printf("data:"); for (int i = 0; i < 10; i++) { printf("%d ", array[i]); } printf("\r\n"); test_qsort(array, sizeof(array)/sizeof(uint16_t),sizeof(uint16_t), CompareFunction); //进行排序 printf("after sort:"); for (int i = 0; i < 10; i++) { printf("%d ", array[i]); } } int CompareFunction(const void* a, const void* b) { if (*(uint16_t*)a - *(uint16_t*)b > 0) return 1; else return 0; } void test_qsort(void* base, uint8_t numofElement, uint8_t sizeofElement, strcmp_fun CompareFunction) { uint8_t L = 0; uint8_t R = numofElement - 1; while (L < R) { while (CompareFunction((unsigned char*)base + (R * sizeofElement), (unsigned char*)base) > 0 && L < R) //array[R] > base { R--; } while (CompareFunction((unsigned char*)base + (L * sizeofElement), (unsigned char*)base) <= 0 && L < R) //array[L] <= base { L++; } for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement) + i; unsigned char* buf2 = (unsigned char*)base + (R * sizeofElement) + i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; } } for (int i = 0; i < sizeofElement; i++) { unsigned char temp = 0; unsigned char* buf1 = (unsigned char*)base + (L * sizeofElement) + i; unsigned char* buf2 = (unsigned char*)base + i; temp = *buf1; *buf1 = *buf2; *buf2 = temp; } if (base < (unsigned char*)base + (L * sizeofElement)) test_qsort(base, L, sizeofElement, CompareFunction); if ((unsigned char*)base + (R * sizeofElement) < (unsigned char*)base + (numofElement - 1) * sizeofElement) test_qsort((unsigned char*)base + (R + 1) * sizeofElement, numofElement - L - 1, sizeofElement, CompareFunction); }
测试成功,目标达成!如果各位大佬有什么更好的建议或者我有什么代码上的错误,欢迎在评论区一起讨论!