分享一种通过二分法快速查找数组中缺失数字的方法
-
最近在看《编程珠玑》提升自己的C语言编程能力,书中的第二章提出了一个有趣的问题。
该问题的描述如下:给定一个最多包含40亿个随机排列的32位整数的顺序文件,找出一个不在文件中的32位整数(在文件中至少缺失一个这样的数--为什么?)。在具有足够内存的情况下,如何解决该问题?如果有几个外部的“临时”文件可用,但是仅有几百字节,又该如何解决问题。
对于为啥文件会确实一个32位的数,这个是显而易见的,我们知道2^32次方是4,294,967,296这个数大于40亿,所以40亿个数是无法完全包含32位整数的全部的。至于,这里有40亿个数,我们怎么找到究竟缺失了哪几个数,这是这个章节考察的重点。我们能不能通过遍历的办法,通过一个基准值然后对比40亿个数,如果能比对成功就证明存在,如果比对不成功,就证明这个数是当前文件所确实的,这个方法当然是可以的,但是在实施是完全不现实的。每比对一个数,就要遍历40亿次(注意,文中指出数据是无序的),所以基本上都要大范围遍历,还要遍历40亿次,这对计算机的性能消耗是巨大的,计算时间也是不可想象的。能不能缩少遍历次数呢,书本提到了位图的方法,通过创建一个大的数组,每个数组的每个位,1代表该数存在,0代表该数不存在,这样,遍历一次即可把位图填满,然后我们再遍历一次位图,看看哪个是0,即可知道究竟是缺失了哪一个数,那这个方法确实可以大大提升计算效率,但是,我们的问题还有一个限制条件,即是内存是有限的,我们很难一次创建一个很大的位图,快速完成遍历。通过理论计算可知,4,294,967,296/8=536,870,912,创建一个完整位图,需要超过500MB的内存,书中最后提出了一个二分搜索的方法。
位图法的原理如下:
1、首先我们先创建一个位图(本文以32位为例子说明),随后将其整个位图初始化为0:
代码如下,比较简单
首先宏定义,
#define N 31
#define BITWORD 8
uint8_t test_array[N / BITWORD + 1] = { 0 };
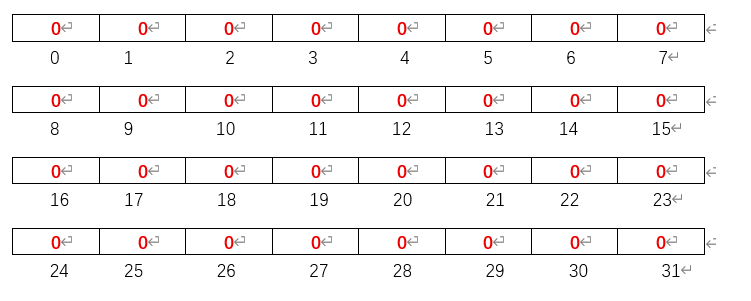
随后,我们可以设计位图操作函数,分别是:
void set_bit(uint8_t* array, uint8_t num);//将位图相关位置置1
void set_bit(uint8_t* array, uint8_t num)
{
array[num >> 3] |= (1 << (num & 0x7));
}
void clear_bit(uint8_t* array, uint8_t num);//将位图相关位置置0
void clear_bit(uint8_t* array, uint8_t num)
{
array[num >>3] &= ~(1 << (num & 0x7));
}
其中右移动三位是指,将要填入的数字除以8(毕竟我们是8位数组),我们先看看把该数字安放在哪个数组,随后我们num&0x7,这个意思是指求他的余数,即是num%0x7,我们可以计算出,该数字在数组应该右移多少位,为了程序设计方便,我们可以通过宏定义替换。
#define SHIFT 3
#define Mask 0x7
void set_bit(uint8_t* array, uint8_t num)
{
array[num >> SHIFT] |= (1 << (num & Mask));
}
void clear_bit(uint8_t* array, uint8_t num)
{
array[num >> SHIFT] &= ~(1 << (num & Mask));
}
我建议做这种除法或取模运算时,尽量运用移位的方法,按位与的方法,这样计算效率会高一些。
假设我们将数字22所在的位置值换为1,
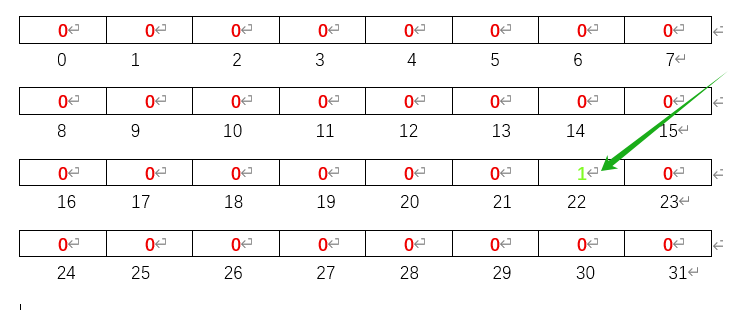
首先,我们通过array[num >> SHIFT],求出我们是将array[2]中的某一位置为1,那究竟是哪一位呢?我们通过num&Mask可以得出是array[2]右移动6位置一,因此我们的置一成功。
接下来,进入到验证部分,
我设计了一个函数:
bool test_bit(uint8_t* array, uint8_t num);//通过判断数字的相应位是否为1,判断该数字是否存在,返回值为布尔量
bool test_bit(uint8_t* array, uint8_t num)
{
return array[num >> SHIFT] & (1 << (num & Mask));
}
当我们输入22时,该函数会判断array[2]的第6位是否为1,进而判断我们是否写入过该数字。下面我们演示一下运行结果:


假设我们改为23,
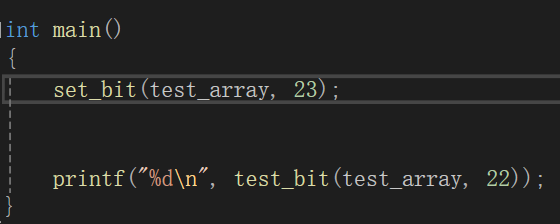

输出符合预期。源代码如下:
#define BITWORD 8
#define SHIFT 3
#define N 32
#define Mask 0x7
void set_bit(uint8_t* array, uint8_t num);
void clear_bit(uint8_t* array, uint8_t num);
bool test_bit(uint8_t* array, uint8_t num);
uint8_t test_array[N / BITWORD + 1] = { 0 };int main()
{
set_bit(test_array, 22);printf("%d\n", test_bit(test_array, 22));}
void set_bit(uint8_t* array, uint8_t num)
{
array[num >> SHIFT] |= (1 << (num & Mask));
}void clear_bit(uint8_t* array, uint8_t num)
{
array[num >> SHIFT] &= ~(1 << (num & Mask));
}bool test_bit(uint8_t* array, uint8_t num)
{
return array[num >> SHIFT] & (1 << (num & Mask));
}
我们可以通过位图法,读取文件中的数字,将位图相应位置置一,随后通过我们设计的验证函数,看看该数是否存在,如不存在,就可以输出该数据,但正如之前分析,该方法需要的内存呢非常大。
下面我们介绍一下,该问题的解决方法,二分查找法,为了演示方便,我们假设存在一个数组,里面的数据在0-16之内,即是4位的数据。那么我们应该如何找到4位数据中的,缺失的数字呢?这里简要介绍一下思路,示意图图下
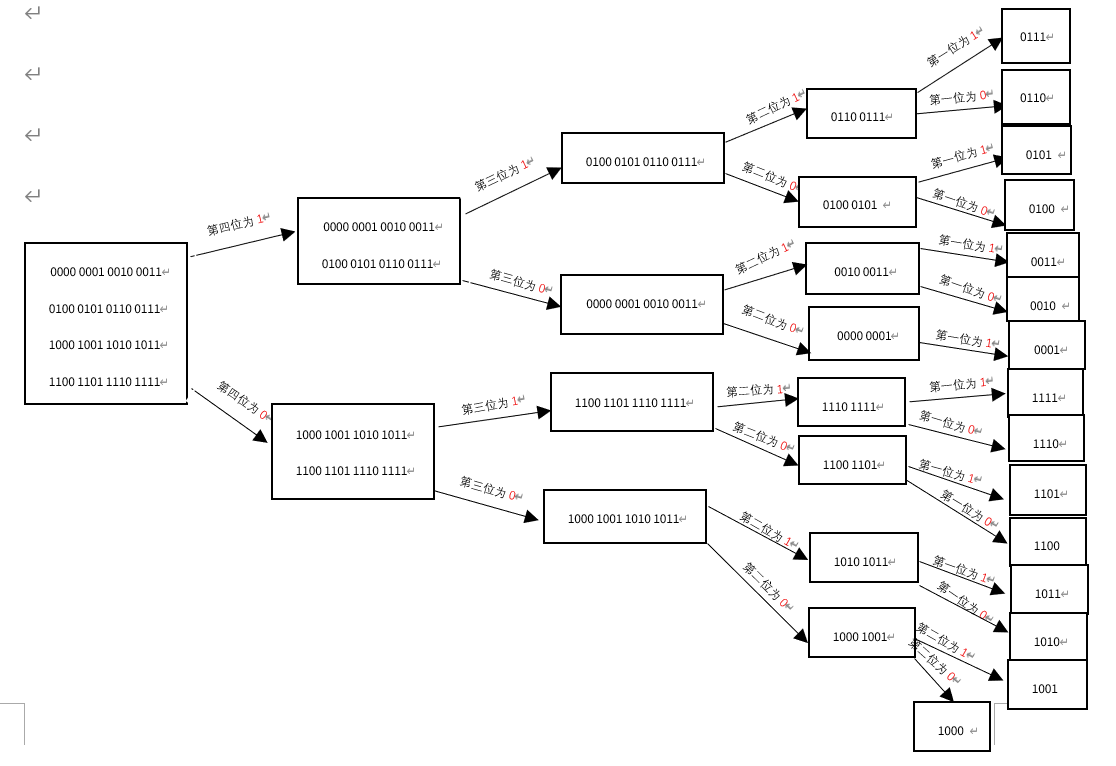
假设我们有16个数,0000,0001,0010,0011,0100,0101,0110,0111,1000,1001,1010,1011,1100,1101,1110,1111,我们发现,这四位数,高位不是1,就是0,通过划分高位0和1,我们可以产生以上的树状图,比如说,第四位为1时,可以分为1000,1001,1010,1011,1100,1101,1110,1111,第四位为0时,可以分为0000,0001,0010,0011,0100,0101,0110,0111,细心观察,我们可以发现,第四位为1时,在0-15的范围内,可以分为0-7,8-15两个区间,此时,我们可以进一步细分,在8-15的区间内,第三位为1时,区间为12-15,第三位为0时,区间为8-11,在0-7区间内,第三位为1时,区间为4-7,第三位为0时,区间为0-3,依次类推,通过这种二分法,可以快速得到各个区间的数字所在区域。同时,我们可以利用原理,快速排查区间中缺少的数字,我们利用递归法,从原始数据开始进行分类,0-15中,假如第四位为1,没能在数组得到数字时,证明,8-15的区间的数字全部缺失,我们可以快速得到数组中缺失的数字,假如第四位为0没能在数组得到数字时,证明0-7的数字全部缺失,当然,有时候,缺失的数字没有那么多,高四位为1和高四位为0都能找到相应的数字,### (需要注意的是,经过上一次的分类,这时候,我们已经分别得到第四位为1和第四位为0的数字分别构成的两个数组,我们需要在此基础进一步细分查找)###,在0-7的区间内,分别查找第3位为1和第3位为0的数字,假如第三位为1的数字没有找到,证明缺失4-7的数字,假如第3位的数字没有找到,证明缺失0-3的数字,假如他们都有,我们可以将搜索到的数字,分别归为4-7和0-3两个数组,进入下一轮搜索,直到搜索到没有相应的数据,进行返回,依次类推,我们从判断第四位为1或零,一直搜索到第一位是1或0,总能把缺失的数据找出来。
我们以0-15的数组中,缺少5和缺少11,10为例
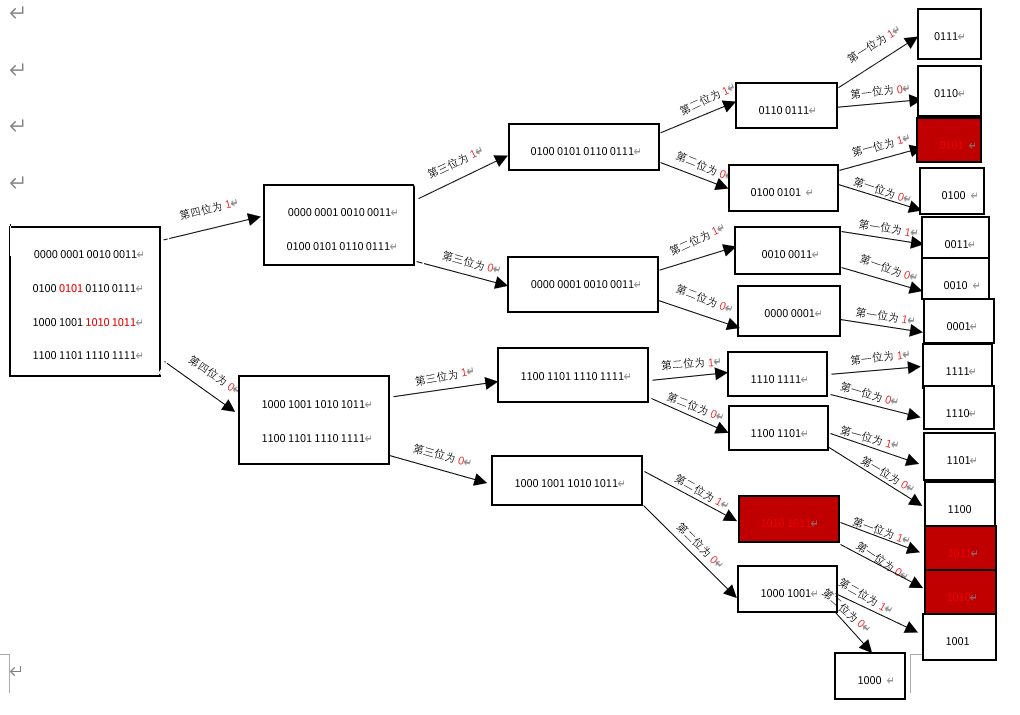
当我们通过二分法,不断细分划分区间时,在{4,5}区间内通过划分第四位为0或1,我们可以找到,我们的数字5是缺失的,通过{8,9,10,11}通过划分第二位为0或1,我们可以找到,10和11是缺失的,一次找出了两个缺失数字,这就是二分法的高明之处。下面,我们演示一下代码运行的结果:
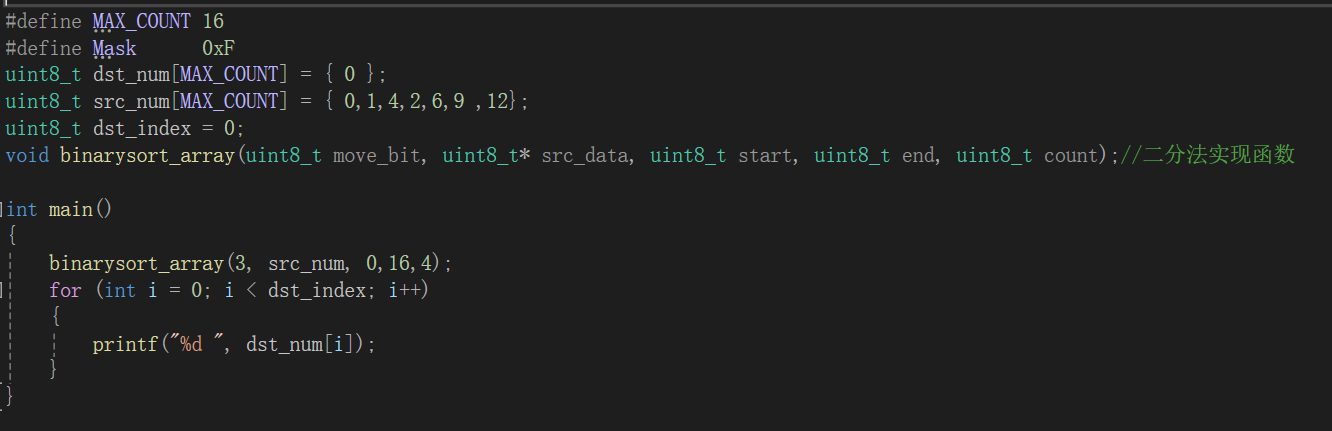
创建数组,源数组src_data有{0,1,4,2,6,9,12}7个数字,我们同时创建一个数组,src_data记录缺失的数字,并打印出来,运行结果如下:

结果运行正确。下面我们贴出实现代码过程:
#define MAX_COUNT 16
#define Mask 0xF
uint8_t dst_data[MAX_COUNT] = { 0 }; //目标数据(缺失的数字)
uint8_t src_data[MAX_COUNT] = { 0,1,4,2,6,9 ,12}; //源数据
uint8_t dst_index = 0;
void binarysort_array(uint8_t move_bit, uint8_t* src_data, uint8_t start, uint8_t end, uint8_t count);//二分法实现函数int main()
{
binarysort_array(3, src_data, 0,16,4);
for (int i = 0; i < dst_index; i++)
{
printf("%d ", dst_data[i]);
}
}void binarysort_array(uint8_t move_bit, uint8_t* src_data, uint8_t start,uint8_t end,uint8_t count)
{
uint8_t Bit_zero_array[MAX_COUNT] = { 0 }; //存储Bit位为0的数组
uint8_t Bit_one_array[MAX_COUNT] = { 0 }; //存储Bit位为1的数组
uint8_t Bit_zero_index = 0;
uint8_t Bit_one_index = 0;for (int i = 0; i < count; i++) { if (((src_data[i] >> move_bit) & 0x1) == 1) { Bit_one_array[Bit_one_index++] = src_data[i]; //将源数据分为两个区间,此为Bit为1的区间,并用Bit_one_index记录其数量 } else { Bit_zero_array[Bit_zero_index++] = src_data[i]; //将源数据分为两个区间,此为Bit为0的区间,并用Bit_zero_index记录其数量 } } if (Bit_one_index == 0) //假如Bit为1的数目等于0,证明区间相应的数字缺失 { for (int i = (start+end)/2; i < end; i++) { dst_data[dst_index++] = i; } } else if (Bit_one_index != 0 && move_bit > 0) //将Bit为0的数组送入下一轮筛选 { binarysort_array( move_bit-1, Bit_one_array, (start+end)/2,end, Bit_one_index);//不断细分区间 //8-15 (start+end)/2,end //12-15 //4-7 //14-15 //10-11 //6-7 //2-3 } if (Bit_zero_index == 0) //假如Bit为0的数目等于0,证明区间相应的数字缺失 { for (int i = start; i < (start+end)/2; i++) { dst_data[dst_index++] = i; } } else if (Bit_zero_index != 0 && move_bit > 0) //将Bit为1的数组送入下一轮筛选 { binarysort_array(move_bit - 1, Bit_zero_array, start,(start+end)/2, Bit_zero_index); //不断细分区间 //0-7 start,(start+end)/2 //0-4 //8-11 //0-1 //4-5 //8-9 //12-13 }}
以上就是我关于该问题的一些个人心得,欢迎各位大佬提出建议,不吝赐教! -
例如文中的代码
#define BITWORD 8 #define SHIFT 3 #define N 32 #define Mask 0x7 void set_bit(uint8_t* array, uint8_t num); void clear_bit(uint8_t* array, uint8_t num); bool test_bit(uint8_t* array, uint8_t num); uint8_t test_array[N / BITWORD + 1] = { 0 }; int main() { set_bit(test_array, 22); printf("%d\n", test_bit(test_array, 22)); } void set_bit(uint8_t* array, uint8_t num) { array[num >> SHIFT] |= (1 << (num & Mask)); } void clear_bit(uint8_t* array, uint8_t num) { array[num >> SHIFT] &= ~(1 << (num & Mask)); } bool test_bit(uint8_t* array, uint8_t num) { return array[num >> SHIFT] & (1 << (num & Mask)); }